
一、直角坐标系的概念
直角坐标系由坐标原点和三条相互垂直的坐标轴组成。并规定坐标原点的值为(0,0,0),假设水平向右为X轴正方向,水平向前为Y轴正方向,垂直向上为Z轴正方向。
把一个三维实体放置于直角坐标系中,实体中的每一个点都对应着唯一确定的坐标值。
二、投影的概念
投影是物体或图形的影子投射在一个面上或一直线上。按照光源的不同,可以分为中心投影和平行投影。中心投影是使用点光源对物体形成的投影(见图3-9)。平行投影是使用平行光源对物体形成的投影,也称正投影(见图3-10)。

图3-9 中心投影
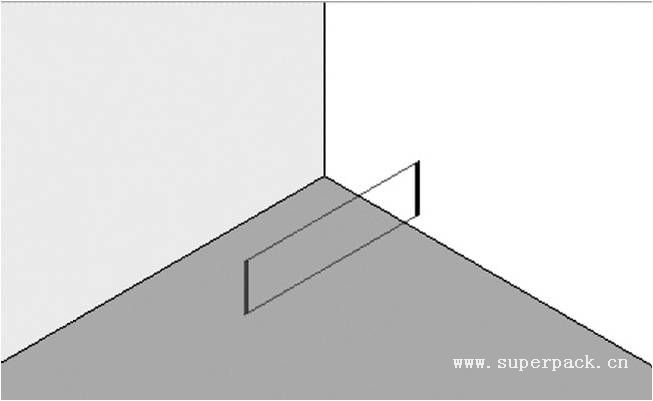
图3-10 平行投影
中心投影立体感强,与肉眼感受接近,主要应用在绘画、艺术领域。平行投影反映事物的真实大小,容易实现事物重现和加工,主要应用在机械、工程领域。
按照视点的不同,投影方法可以分为第一角投影法和第三角投影法。目前,美国、日本及大多数欧盟国家使用的是第三角投影法(见图3-12),而中国官方使用的是第一角投影法(见图3-11)。
第一角投影法把三个视图分别称为:主视图、俯视图、左视图。
第三角投影法把三个视图分别称为:前视图、顶视图、右视图。
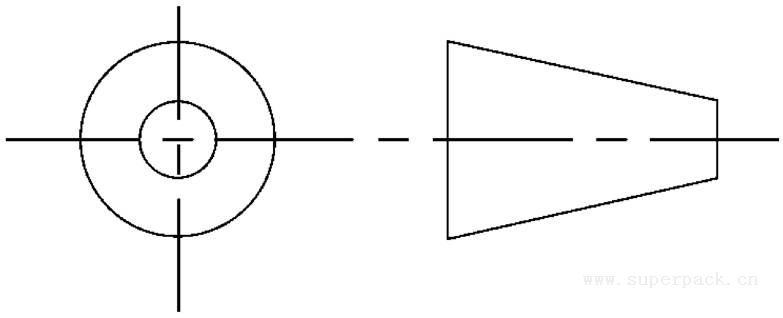
图3-11 第一角投影法
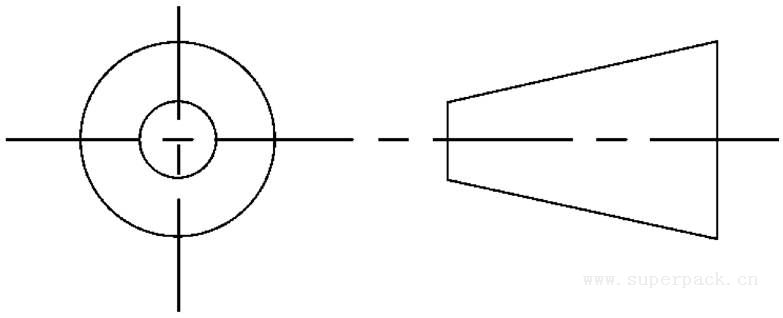
图3-12 第三角投影法
基本投影方法有点的投影、线段的投影、平面的投影、曲面的投影以及实体的投影,以下将分别介绍。
(1)点的投影。点在三个坐标平面上的投影分别等于它在坐标系中的XZ、XY、YZ坐标值所对应的点(见图3-13)。
(2)线段的投影。线段在三个坐标平面上的投影分别等于它的两个端点的投影所组成的线段(见图3-14)。
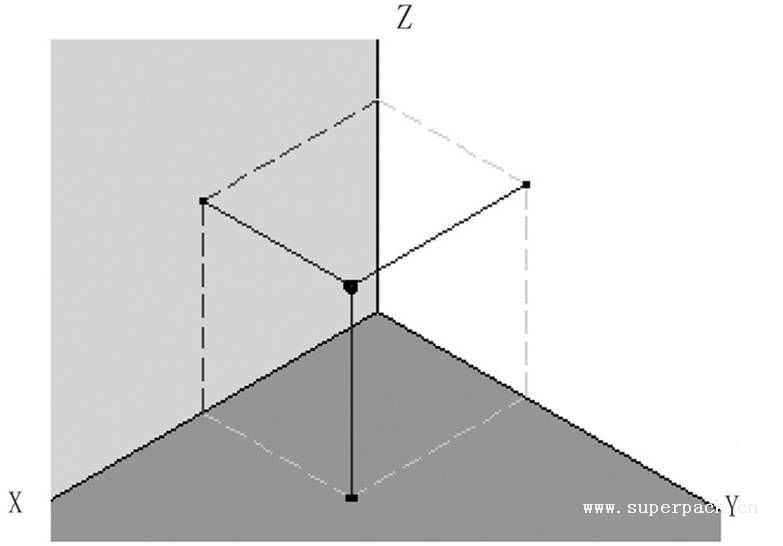
图3-13 点的投影
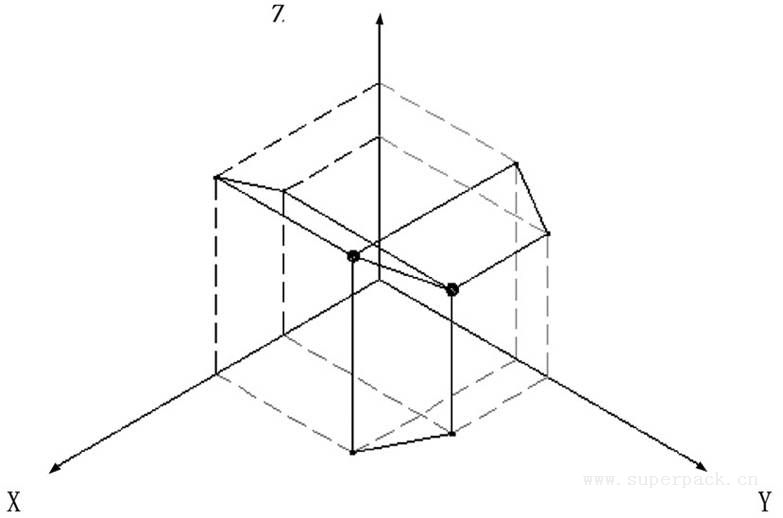
图3-14 线段的投影
(3)平面的投影。平面通常用确定该平面的点、直线或平面图形等几何元素的投影表示,根据平面在三投影面体系中的位置可分为投影面垂直面、投影面平行面和投影面倾斜面(见图3-15)。
(4)曲面的投影。曲面在三个视图上的投影等于组成曲面边界线的投影以及与投影面垂直的切线的投影之和(见图3-16)。
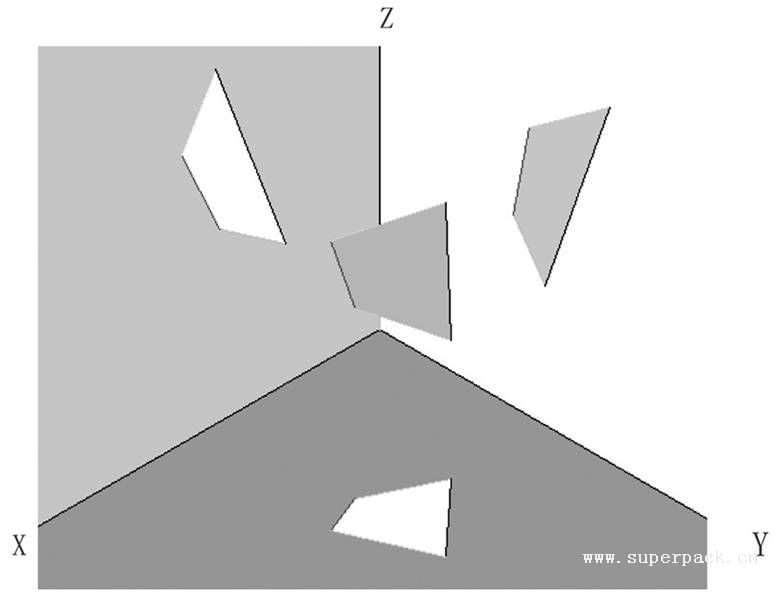
图3-15 平面的投影
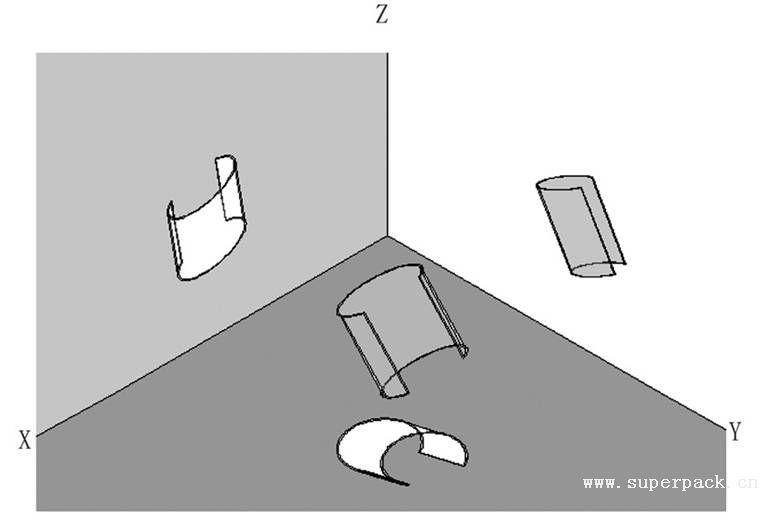
图3-16 曲面的投影
(5)实体的投影。实体在三个视图上的投影等于组成实体各表面的投影之和(见图3-17)。
点的投影还是点,线的投影还是线。平面的投影只有周围的边界线,平面中间的点没有投影。曲面的投影有周围的边界线,曲面中间大部分点都没有投影,只有与投影面有垂直切线的点才有投影。实体的投影只有表面有投影,实心内部的点没有投影。
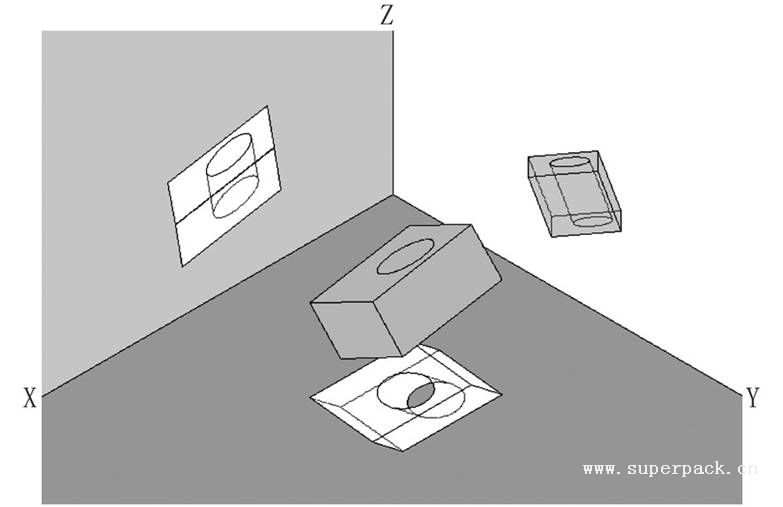
图3-17 实体的投影
直线在垂直于直线的平面上的投影为一个点。平面在与之垂直的平面上的投影为一条线。圆柱体在与圆柱端面平行的平面上的投影为一个圆。球体在任何平面上的投影都是一个圆。
为了便于看图、绘图、尺寸标注以及方便生产加工,通常选择最能表达形体的方向进行投影,尽可能把平面投影成线,把圆柱面投影成圆。
三、视图
视图是采用平行投影的方法,将物体投射到特定平面上所形成的图形(见图3-18)。一个视图可以反映物体两个方向的尺寸,三个不同方向的视图可以反映物体所有的尺寸。三视图是将一个物体三个相互垂直方向的视图展开对正放置在一起。
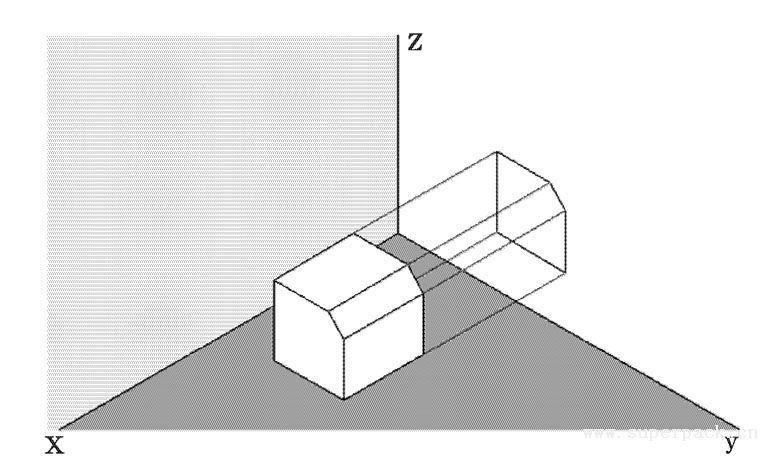
图3-18 视图
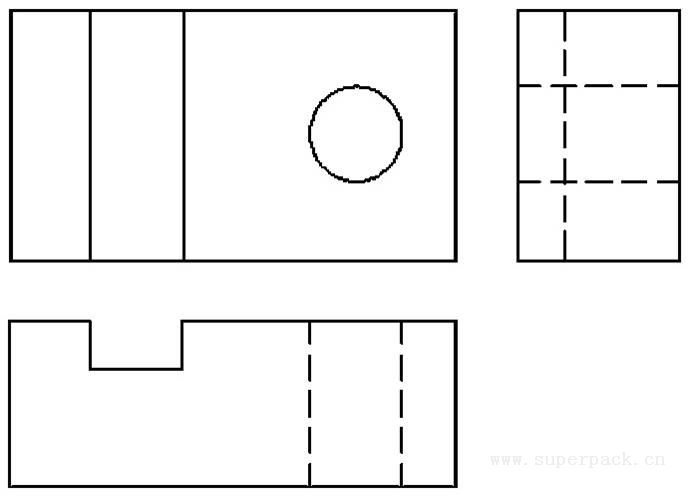
图3-19 三视图示例
三视图是表达复杂三维实体的重要方法(见图3-19)。实际上,很多物体并非在三个投影方向都很复杂,我们只需要使用两个甚至一个视图就可以完整地表达。
只使用一个视图的,我们通常称为平面图(见图3-20)。例如建筑平面图、板金件展开图等。一般的纸盒、纸箱展开图就是使用的这种方法。
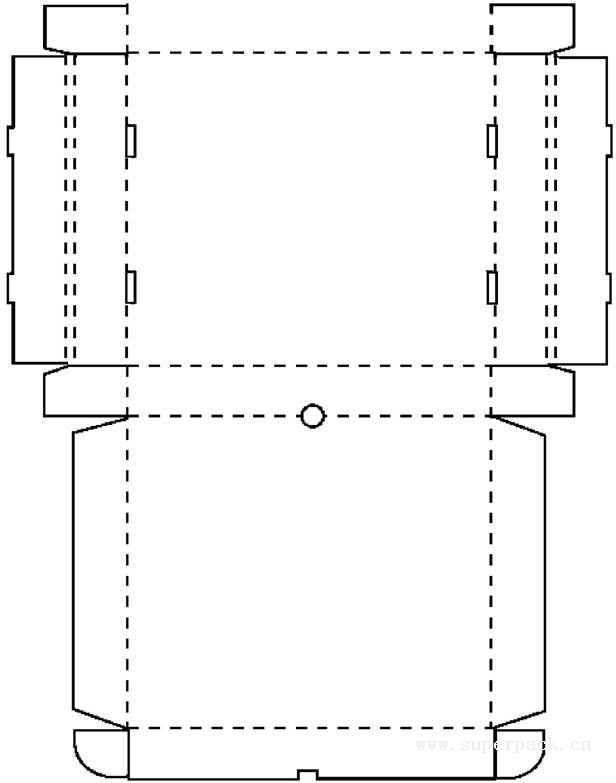
图3-20 平面图示例
四、正轴测图简介
正轴测图分为正等测图和正二测图。在正轴测投影图中,当三个轴向变形系数相等时,称为正等测投影(见图3-21);当三个轴向变形系数中有两个相等时,称为正二测投影(见图3-22)。
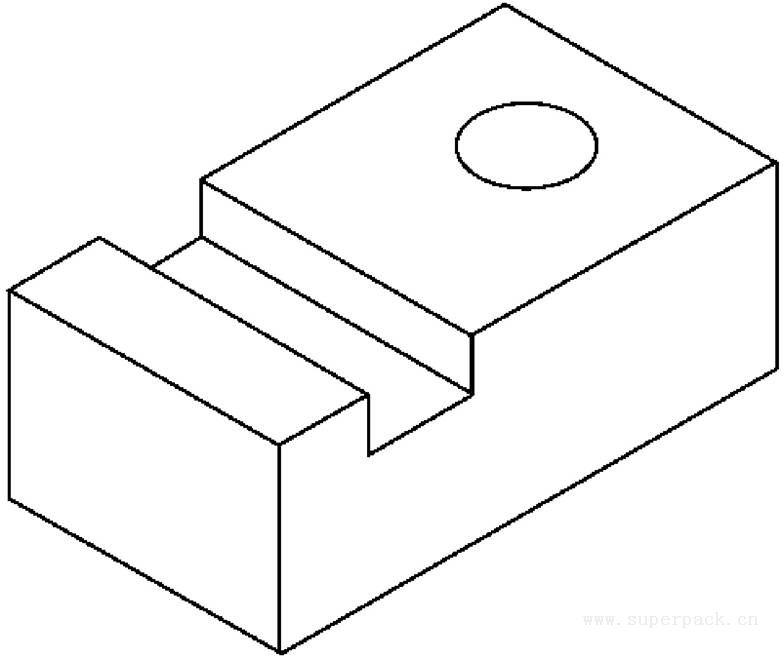
图3-21 正等测图
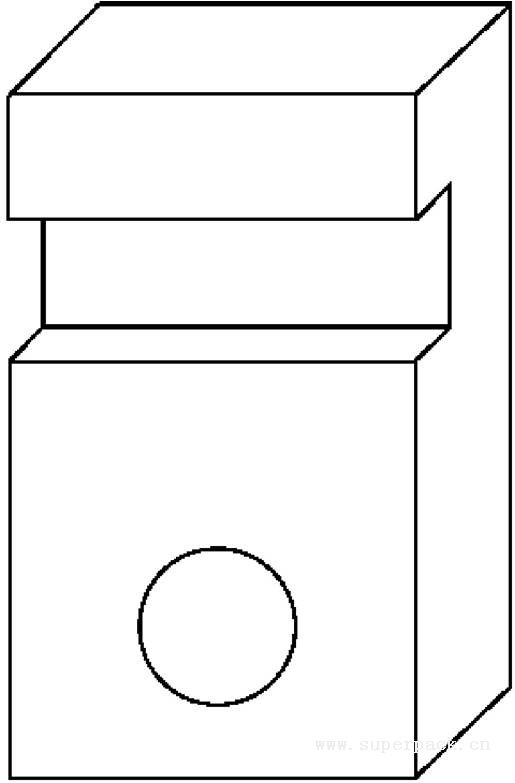
图3-22 正二测图







